ニュートンの業績 1687年 自然哲学の数学的諸原理(プリンキピア) Philosophiae Naturalis Principia Mathematica 微分積分を用いず幾何学的に記述している。 ラテン語で書かれている。 ニュートン力学を完成させた著書。その他様々な命題を含む。 微分積分の論文は?コペン) ことは当然だろう さて, (B1) デカルト哲学はデカルト座標と関係するのか? は愚問であるニュートン力学と微分方程式の意味がわかる 万有引力から相対論的力学まで ここまでニュートン力学を徹底的に掘り下げた一般書はありません!
Q ビセキブン とは何のことですか A 魔法です
微分 ニュートン
微分 ニュートン-ニュートンの記法 (にゅーとんのきほう、 英 Newton's notation )は、 数学 における 微分の記法 のひとつである。 · 生涯イギリスを出なかった大学教授ニュートン 1642年、ニュートンはイギリス中部のウールスソープという小さな村の農家に生まれました。叔父の援助を受け、1661年からケンブリッジ大学に入学します。 しかし、1665年頃にペストが大流行。大学は閉鎖され、故郷の村に帰らなければな



ライプニッツとニュートン なぜ差がついたか それは 記号 だ 佐藤 恒雄 ブルーバックス 講談社 1 2
微分方程式 第 回 7 14 モデル化:分離可能な方程式 例3 暖房の問題(ニュートンの冷却の法則) 就寝の2時間前に家の暖房を切る。この時刻を =0と高橋, 秀裕(1954) 言語 日本語(2)式を用いると、ニュートンの運動方程式(1)は、 m d⃗v dt = F⃗ (3a) あるいは m d2⃗r dt2 = F⃗ (3b) とも表せる。(3a)式や(3b)式は、数学的には微分方程式と呼ばれる。物体の速度⃗v や位置⃗r を求め ることは、数学的には微分方程式を解く(=積分する)作業で
= #(!) (*は積分定数) 17世紀の物理学者アイザック・ ニュートンは「微分と積分」の 関係が自然界を記述する基本的 なルールであると気づき、微積 分学という新しい数学を生み出 しました。 ウィーン⾃然史博物館のニュートン像ニュートン法(ニュートン・ラフソン法) とは︖ 非線形方程式f(x) = 0 を数値的に解く方法の1つ 微分可能な方程式であれば、たとえ微分しなくても解が求まる 繰り返し計算により解に近づく 初期値を変えて何回か解く方がよい 1微分と積分 ニュートンの大発明 これならわかる (ニュートンムック サイエンステキストシリーズ)(自然科学・環境) 天才科学者アイザック・ニュートンは、どんなことを考えて、微分・積分をつくりだすことになったのか。一見すると複雑な微分・積分の記号や計算方法に紙の本の
· アイザック・ニュートン Sir Isaac Newton アイザック・ニュートンは、イギリスの数学者・物理学者、古典力学を確立した。主著『プリンキピア』。1642年、12月25日、イギリスのリンカンシャーでニュートンが生ま2 ニュートンの運動方程式 8 そして、L をx とx_ で微分する。 @L @x = dV dx @L @x_ = mx_ ∴ d dt (@L @x_) = m x よって、ニュートンの運動方程式から次の式が導かれる。 d dt (@L @x_) @L @x = 0 この式を、ラグランジュの方程式という。これは、ニュートンの運動方程式と同値である。そして、ニュートンの記法(にゅーとんのきほう、英 Newton's notation )は、数学における微分の記法のひとつである。 この記法は アイザック・ニュートン が fluxion ( 流率・流動率 ) 1 と呼称した 時間 に対する変化率を表すために導入したもので、 関数 名の上部



微分導入時の雑談 怜悧玲瓏 高校数学を天空から俯瞰する



メルカリ ニュートン Newton 微分と分析 これならよくわかる 健康 医学 500 中古や未使用のフリマ
言うと「微分方程式」という考え方の有無である といえる。そもそもニュートンにとっては,微分 積分と力学は一体であったにも拘らず,高校の物 理教科書ではそれに触れてはならないという不合 理が今もまかり通っている。その結果,例えば速ニュートン力学は微分方程式論, 相対性理論は微分幾何学とそれぞれ関係する また, 量 子言語は作用素代数と関係する(cf 文献KOARA 18;• ある点x nでの導関数f'(x n)が与えられるとき、!


微分積分 運動を語る数学の共通言語 空間情報クラブ 株式会社インフォマティクス



Newton別冊 微分と積分 新装版 ニュートン別冊 本 通販 Amazon
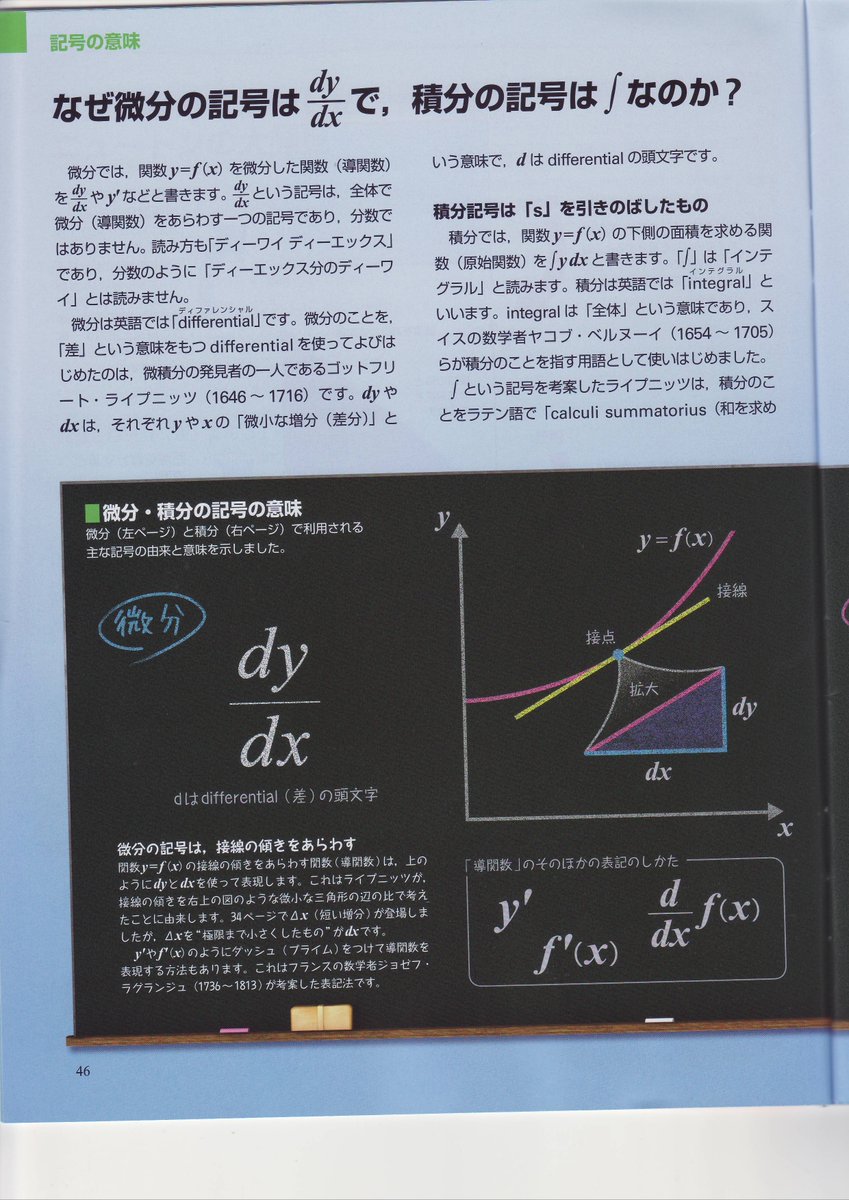
ニュートン、ライプニッツによる微分積分法の創始 イギリスのニュートンは、f(x,y)をx、yの多項式としてf(x,y)=0という曲線上を動く点を考えた。そして、この点の水平方向の速さ、垂直方向の速さをそれぞれ 、 で表し、これらをx、yの流率とよんだ。 この流率の比 / は接線の傾きでありを,関数 y = f(x) の導関数(または微分)といいます。 −−−−−−−− 導関数(微分)はニュートンとライプニッツが別々に考え出したと言われ,導関数を表わす記号も,ニュートンの記号 y', f'(x) と,ライプニッツの記号 ,ニュートンが太陽系の運動法則を証明するのに使ったのが微分積分なのです。 微分積分は、ニュートン力学を証明する手段として誕生したといっても過言ではありません。 それくらいに、物理学や力学に密接に関係したものなのでした。 微分積分を簡単に言いますと、その方法は先述したデカルトの四つの法則の中の二番目と三番目に当たります。 二番目は



ニュートンの記号を使う 17 怜悧玲瓏 高校数学を天空から俯瞰する



楽天ブックス ニュートンとライプニッツの微分積分 離散と連続から考える 研伸館 本
ライプニッツとニュートン:微積分学発見の優先権論争 ライプニッツはデカルトやパスカルと同様、数学や自然科学の分野においても顕著な業績を残した。 とりわけ数学の分野においては、微分積分学と記号論理学の創始者として、歴史的な業績を上げた。 ライプニッツが微分法の研究に打ち込んだのは、パリに滞在していた1675年から76年にかけてであるが、彼が · アイザック・ニュートンによるニュートンの記法は微分のドット記法とも呼ばれ、従属変数の上部にドット記号「・」を記して =, =, などのように表す。しばしば速度や加速度のような時間微分の表現法として使用される。方程式cos(x)=x2 の解をニュートン法によって解くプログラムを f ′ (x)=−sin(x)−2x の計算箇所を数値微分を用いて書け. 初期値 x (0) としては 10 を取り,表記は以下のようにせよ.



ニュートンの記号を使う 17 怜悧玲瓏 高校数学を天空から俯瞰する



微分の表記方法 Dy Dxのdって何 物理のいろは
微分記号の記法としては といったライプニッツの記法が一般的です。しかし力学系等の分野によっては のようなニュートンの記法の方が好まれる場合もあります。 文字の右側にカーソルを位置付け右クリック、「プロパティ」と操作することによって= ((!)* (′ !1.微分作用素のニュートン図形とは? 複素平面C の原点に特異点を持つ解析的常微分作用素次のように書きます。 (1) P = ∑m j=0 aj(z) d dz)j, am(0) = 0, am(z) ̸≡0 ここで、rj = O(aj), 即ち、aj(z) = zrjbj(z) (bj(0) ̸= 0) とします。 このとき、微分作用素と座標平面R2 内の図形との間の対応を考えます。



微分 ニュートンと学ぶ微分 大人が学び直す数学



ニュートンの記号を使う 17 怜悧玲瓏 高校数学を天空から俯瞰する
微分と積分 ニュートンの大発明 フォーマット 図書 責任表示 水谷, 仁(1942) ;本書は,この現代人の必修科目ともいうべき微分・積分を総特集したNewton別冊『微分と積分 新装版』の改訂版です。 知識ゼロからでも楽しく読み進めていただけるよう,微分・積分のエッセンスをやさしく解説した特集記事を新たに収録しました。 このほかにも,微分・積分を誕生させた時代背景や数学者たちの思考,微分・積分の計算問題や応用事例なども収録微分法の誕生(ニュートンの流率法) 微分法の誕生(ニュートンの流率法) Watch later Share Copy link Info Shopping Tap to unmute If playback doesn
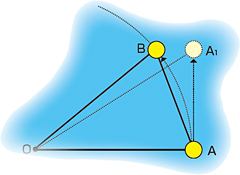


微積分が導いた宇宙の法則 万有引力の発見は数学の賜物 サイエンス テクノロジー 研究 社会連携 京都産業大学



楽天市場 ニュートン 微分 積分の通販
有名なニュートンの運動の法則です。第2法則が所謂運動方程式 に対応します。 微分やベクトルを使う訳(レベル1) (\ref{EOM})式はベクトルの微分方程式です。 なぜ、ベクトルや微分を使う必要がある導関数(微分)はニュートンとライプニッツが別々に考え出したと言われ,導関数を表わす記号も,ニュートンの記号 y', f'(x) と,ライプニッツの記号 ,うさぎでもわかる微分方程式 Part01 変数分離形(1階微分方程式 ニュートンの冷却の法則 倭算数理研究所;



ヨドバシ Com 微分と積分 これならわかるニュートンの大発明 ニュートンムック Newton別冊サイエンステキストシリーズ ムックその他 通販 全品無料配達



Newtonライト 微積のきほん ニュートンプレス
位置の2階微分である加速度が力と質量から決定される。ニュートンは、微分の考えを初め に創始した者でもある。 力学の諸問題は、微分、積分や微分方程式の応用の場としても最適である。本書は、力学 と数学を同時に学ぶよう構成されている。



ヨドバシ Com 微分と積分 新装版 ニュートン別冊 ムック その他 通販 全品無料配達



微分積分単行本ニュートン式超図解最強に面白い 露天拍賣



ライプニッツとニュートン なぜ差がついたか それは 記号 だ 佐藤 恒雄 ブルーバックス 講談社 1 2
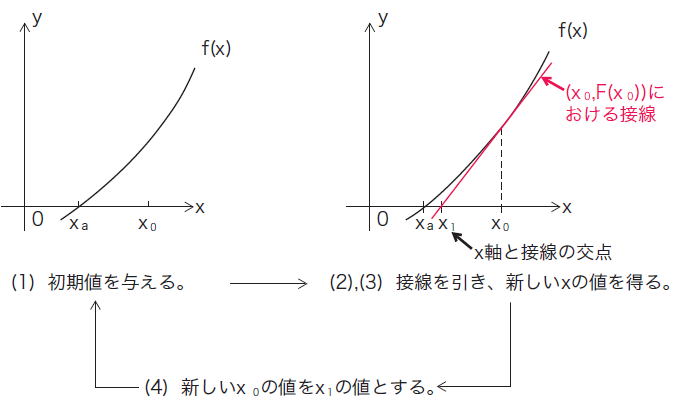


第67回 微分 積分の数学 ニュートン ラフソン法 前編 はじめmath Javaでコンピュータ数学 Gihyo Jp 技術評論社



ニュートンの記号を使う 17 怜悧玲瓏 高校数学を天空から俯瞰する



ニュートンとライプニッツの微分積分 離散と連続から考える 知りたい サイエンス 1 アップ研伸館 編集 吉田信夫 著 古本 中古本 古書籍の通販は 日本の古本屋 日本の古本屋



Newton別冊 微分と積分 新装版 ニュートン別冊 本 通販 Amazon



微分積分学 Wikipedia



楽天市場 ニュートン 微分 積分の通販



Paypayフリマ 微分積分4冊セット マンガでわかる微分積分 大上丈彦 眠れなくなるほど面白い図解 図で考えれば解ける 本当は面白い ニュートン式


セカント法による求根 Thoth Children



力学 微分とnewtonの運動方程式 高校数学



ゆな בטוויטר ニュートンとライプニッツによる微積分学よ発見をめぐる争い ニュートン ライプニッツ 数学史 微分 積分
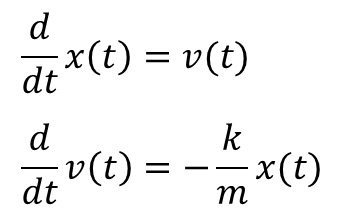


Step 05 2階常微分方程式を解いてみる ニュートン方程式 筑波大学原子核理論研究室



渡辺美優紀 みるきー わるきー 愛するnewtonさんにインタビューしていただきました 7 19発売です 夏は 微分積分についてみんなでお勉強しよう 紙面では宇宙について語っています Newton ニュートン にゅーとん 微分積分



5分でわかる ニュートンの冷却の法則 理系学生ライターがわかりやすく解説 ページ 2 3 Study Z ドラゴン桜と学ぶwebマガジン



No 6 微分と積分 増補改訂版 ニュートンムック Ehomahouse
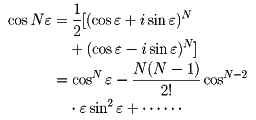


微分積分法とは コトバンク



5分でわかる ニュートンの冷却の法則 理系学生ライターがわかりやすく解説 ページ 2 3 Study Z ドラゴン桜と学ぶwebマガジン



Newton 微分積分の中古 未使用品を探そう メルカリ



Mer ニュートンは微積分学 Calculus をつくり 結石 同じく英語でcalulus で亡くなったのでした Newton別冊 微分と積分 新装版 より そ それは知らなかった というかnewton この別冊シリーズは初めて読みましたが 良いですね 全て揃えたく
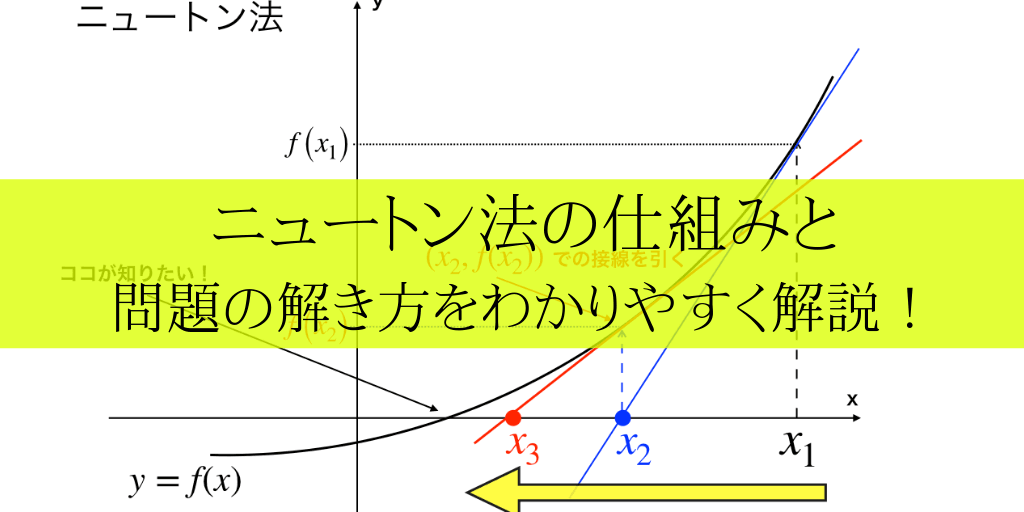


ニュートン法の仕組みと証明の仕方を分かりやすく解説



ニュートンの記号を使う 17 怜悧玲瓏 高校数学を天空から俯瞰する



共立出版 アリがと蟻 Ar Twitter ニュートンプレスさんから 三角関数 と 微分積分 の新刊が発行されましたね 左の本はお馴染み 結城浩先生の 数学ガールの秘密ノートシリーズ Sbクリエイティブさん発行 です 撮影協力 Booksなかだ 掛尾本店 本館



Newton ニュートン 18年 11月号 Newton編集部 Hmv Books Online



楽天市場 ニュートン 微分 積分の通販



ゆな ニュートンとライプニッツによる微積分学よ発見をめぐる争い ニュートン ライプニッツ 数学史 微分 積分



5分でわかる ニュートンの冷却の法則 理系学生ライターがわかりやすく解説 Study Z ドラゴン桜と学ぶwebマガジン



ヨドバシ Com 60分でわかる微分と積分 別冊ニュートン 19年 08月号 雑誌 通販 全品無料配達
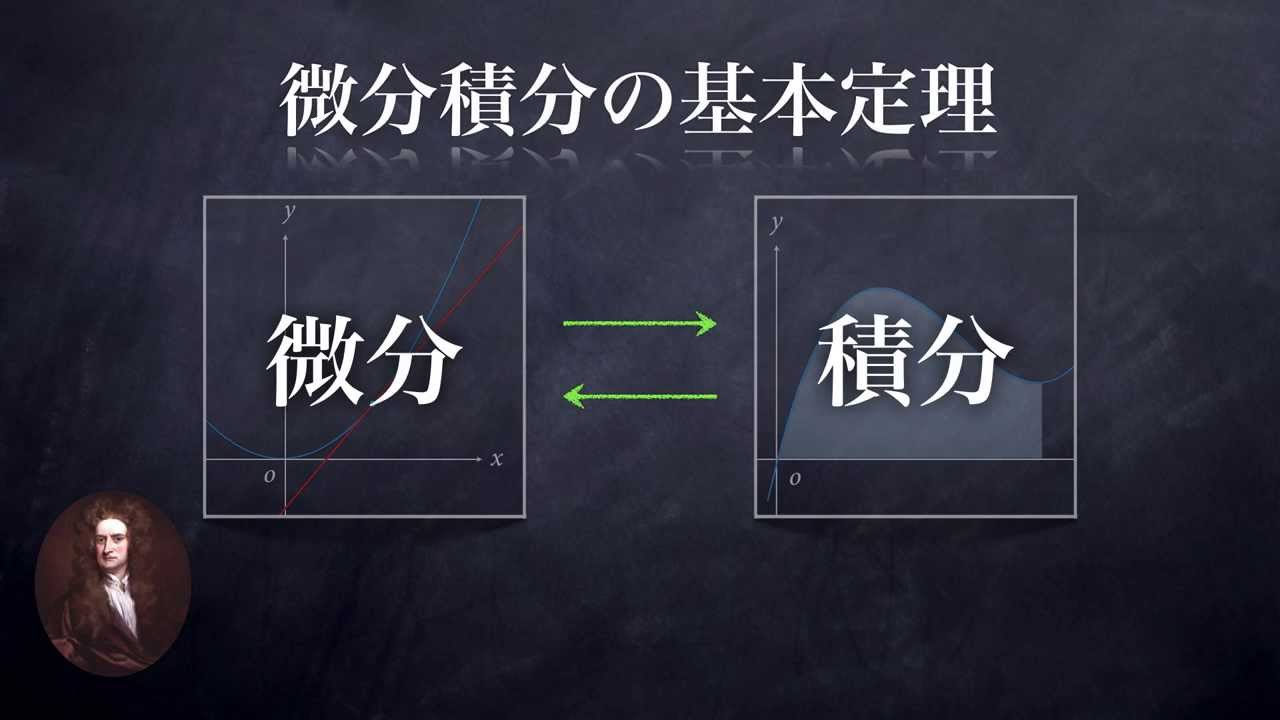


ニュートンの大発見 微分と積分は逆関係 Youtube


ニュートン法とは 制御工学の基礎あれこれ



ニュートンの記号を使う 17 怜悧玲瓏 高校数学を天空から俯瞰する


Q ビセキブン とは何のことですか A 魔法です



微分積分法 を発見した学者が実は二人いた リンゴで有名な物理学者 ともう一人は ナゾロジー



Newtonニュートン増刊vol 1 特集60分でわかる微分と積分 永久保存版特集 ニュートンはどのような思考を経て微分積分を生みだした渡辺美優紀 の落札情報詳細 ヤフオク落札価格情報 オークフリー スマートフォン版


ゼロからの微分と積分 Newton 18 11号 発想法 情報処理と問題解決



Uas02srm1iydfm



ヨドバシ Com 微分と積分 増補改訂版 ニュートンムック ムックその他 通販 全品無料配達



山本貴光 V Twitter Newton 18年11月号 ニュートンプレス も微分積分特集 ニュートン ライプニッツ その他 世界を変えた書物 展に本が出ていたみなさんもご登場


第4回目



Newtonライト2 0 微分積分 ニュートンムック 本 通販 Amazon



8月号増刊 60分でわかる 微分と積分 Newton 増刊 本 通販 Amazon


42 5 ニュートンは何故微分方程式を使わないで プリンキピアを書いたのか 理系の科学哲学 コペンハーゲン解釈 理系の西洋哲学史



最強に面白い 微分積分の通販 髙橋秀裕 紙の本 Honto本の通販ストア



ゆな ニュートンとライプニッツによる微積分学よ発見をめぐる争い ニュートン ライプニッツ 数学史 微分 積分



Newton 微分積分の中古 未使用品を探そう メルカリ



偉大なるニュートンの微分積分や重力の発見は伝染病のおかげ 今週気になったトピックス 仕事編 Mishima Kota Note



Newton 微分と積分の中古 未使用品を探そう メルカリ



微分と積分 微分 科学雑誌newton 数学 Kindleストア Amazon



文系のためのめっちゃやさしい 微分積分 ニュートンプレス



ニュートンの記号を使う 17 怜悧玲瓏 高校数学を天空から俯瞰する



微分積分学 Wikipedia


積分定数 En Twitter 超算数 それから 微積をまだ習ってない中高生にもオススメ とのことですが 微分 積分公式集 重要公式を覚えてセンター試験に挑戦しよう というのを中高生が読んで 公式は覚えるもの と思ってしまわないか心配です



ニュートンの記号を使う 17 怜悧玲瓏 高校数学を天空から俯瞰する



メルカリ ニュートン 別冊 ニュートンの大発明 微分と積分 参考書 1 0 中古や未使用のフリマ



C言語 ニュートン法のプログラムの為の数値微分 Visual Studioでc C言語 C C 教えて Goo



No 6 微分と積分 増補改訂版 ニュートンムック Ehomahouse



無限の問題を解消した 極限 ーそれは100年の努力によって生み出されたー Youtube



微分と積分 ニュートンの大発明 これならわかるの通販 紙の本 Honto本の通販ストア



Newtonライト2 0 微分積分 ニュートンプレス



Paypayフリマ 微分積分4冊セット マンガでわかる微分積分 大上丈彦 眠れなくなるほど面白い図解 図で考えれば解ける 本当は面白い ニュートン式



微分と積分 紀伊國屋書店ウェブストア オンライン書店 本 雑誌の通販 電子書籍ストア



Uas02srm1iydfm



科学雑誌 Newton からよりエンタメな増刊 60分でわかる 微分と積分 が登場 7月19日 金 に全国書店で発売 Sankeibiz サンケイビズ 自分を磨く経済情報サイト



これ以上やさしく書けない微分 積分 ニュートンからの贈り物の通販 小林 吹代 紙の本 Honto本の通販ストア


ニュートン 雑誌 微分積分 数学一般の本 の商品一覧 数学 理学 工学 本 雑誌 コミック 通販 Yahoo ショッピング



メルカリ Newtonニュートン 年12月号 微分と積分 雑誌 850 中古や未使用のフリマ



微分積分で未来予測ができる 科学雑誌newton ニュートン Facebook



ニュートン 反射望遠鏡 微分積分 りんご 万有引力のイラスト素材



単行本 高橋秀裕 ニュートン式超図解 最強に面白い 微分積分の通販はau Pay マーケット Hmv Books Online



遠山啓のコペルニクスからニュートンまで 太郎次郎社エディタス ウェブストア



微分 積分はむずかしくない 科学雑誌newton ニュートン Facebook



微分と積分 増補改訂版 ニュートンムック 本 通販 Amazon



ニュートン力学と微分方程式の意味がわかる 漫画 無料試し読みなら 電子書籍ストア ブックライブ
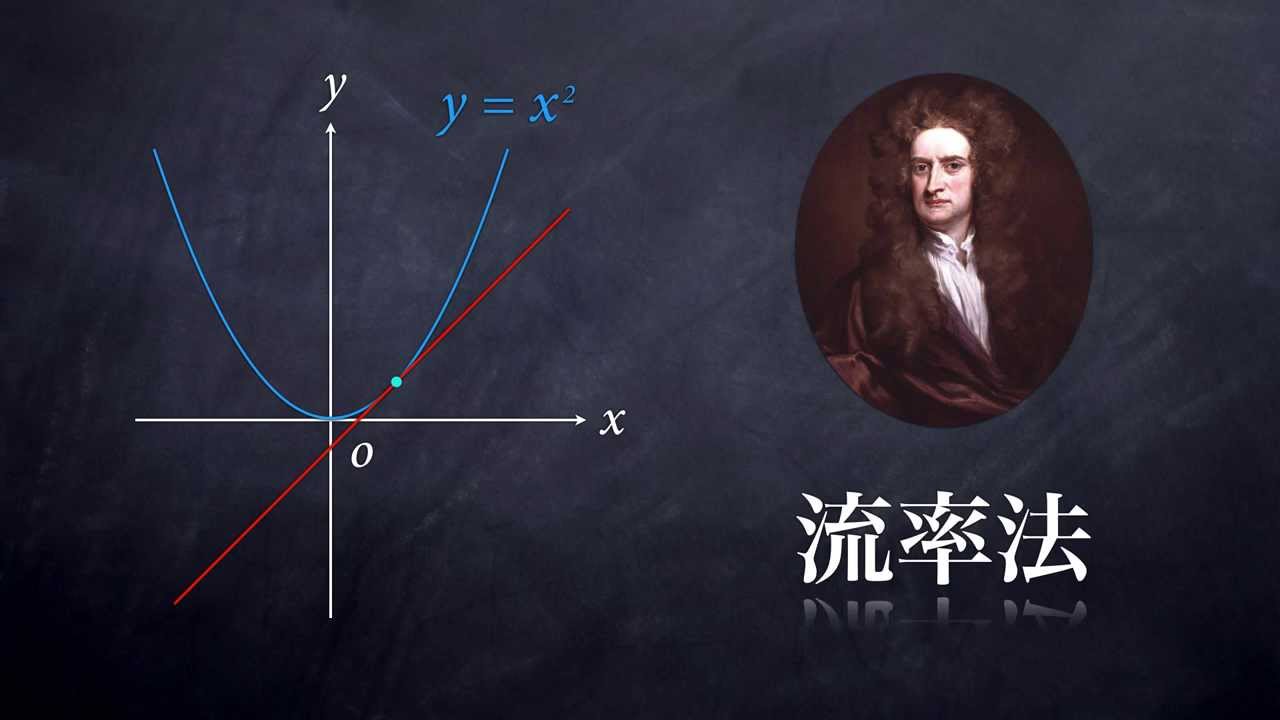


微分法の誕生 ニュートンの流率法 Youtube



ニュートンの記号を使う 17 怜悧玲瓏 高校数学を天空から俯瞰する



Paypayフリマ 微分積分4冊セット マンガでわかる微分積分 大上丈彦 眠れなくなるほど面白い図解 図で考えれば解ける 本当は面白い ニュートン式



楽天市場 ニュートン 微分 積分の通販



Newton別冊 微分と積分 新装版 ニュートン別冊 本 通販 Amazon



微分 微分の表記 ラグランジュ記法とライプニッツ記法 大人が学び直す数学



微分と積分 知識ゼロから考え方が身につく永久保存版 改訂第2版 通販 セブンネットショッピング


微分の表記法にはニュートン表記やライプニッツ表示などがありますが 微分の Yahoo 知恵袋


Q ビセキブン とは何のことですか A 魔法です



科学雑誌ニュートン年12月号 ゼロと微分積分 ニュートンプレス



ニュートン法で方程式の近似解を求める 薬剤師のプログラミング学習日記



微分と積分 改訂第2版 ニュートンプレス



0 件のコメント:
コメントを投稿